- Research Article
- Open access
- Published:
An Extended Image Hashing Concept: Content-Based Fingerprinting Using FJLT
EURASIP Journal on Information Security volume 2009, Article number: 859859 (2009)
Abstract
Dimension reduction techniques, such as singular value decomposition (SVD) and nonnegative matrix factorization (NMF), have been successfully applied in image hashing by retaining the essential features of the original image matrix. However, a concern of great importance in image hashing is that no single solution is optimal and robust against all types of attacks. The contribution of this paper is threefold. First, we introduce a recently proposed dimension reduction technique, referred as Fast Johnson-Lindenstrauss Transform (FJLT), and propose the use of FJLT for image hashing. FJLT shares the low distortion characteristics of a random projection, but requires much lower computational complexity. Secondly, we incorporate Fourier-Mellin transform into FJLT hashing to improve its performance under rotation attacks. Thirdly, we propose a new concept, namely, content-based fingerprint, as an extension of image hashing by combining different hashes. Such a combined approach is capable of tackling all types of attacks and thus can yield a better overall performance in multimedia identification. To demonstrate the superior performance of the proposed schemes, receiver operating characteristics analysis over a large image database and a large class of distortions is performed and compared with the state-of-the-art image hashing using NMF.
1. Introduction
Digital media has profoundly changed our daily life during the past decades. However, the massive proliferation and extensive use of media data arising from its easy-to-copy nature also pose new challenges to effectively manage such abundance of data (e.g., fast media searching, indexing) and protection of intellectual property of multimedia data. Among the various techniques proposed to address these challenges, image hashing has been proven to be an efficient tool because of its robustness and security.
An image hash is a compact and exclusive feature descriptor for a specific image. Robustness and security are its two desired properties [1, 2]. Different from traditional hash, image hash does not suffer from the sensitivity to minor degradations of original data because of its perceptual robustness. Such a property requires two images that are perceptually identical in human visual system (HVS) and are mapped to similar hash values. Obviously, the more robust a hash is, the less sensitive it is to large distortions upon the original images, which in turn inevitably incurs another problem that distinct images may be misclassified to the same group. Hence, tradeoff between robustness and anticollision of distinct images is of great concern. Additionally, by incorporating the pseudorandomization techniques, a hash is hardly obtained by unauthorized adversaries without the secret key. Therefore, the unpredictability encrypts the image hash and guarantees its security against illegal access.
Behaving as a secure tag for image data, image hashing facilitates significant developments in many areas such as image and video watermarking [3]. It is worth mentioning that different applications may impose different requirements in a hashing design. For the purpose of image authentication, it is required that minor unmalicious modifications which do not alter the content of the data should preserve the authenticity of the data [4, 5]. The robustness of image hash assures its capability to authenticate the content by ignoring the effect of minor unmalicious modifications on the original data. For the management of large image databases [6], image hashing allows efficient media indexing, identification, and retrieval by avoiding exhaustively searching through all the entries, thus reducing computational complexity of similarity measurements. Moreover, specific hashing designed based on some specific features of image data, such as color, edges, and other information, obviously contributes to the content-based image retrieval (CBIR) system [7] at the semantic level. In this paper, we are particularly interested in image identification and explore the application of image hashing in this direction.
Although there exist various frameworks to design robust and secure hashes [8–10], a hashing scheme generally consists of two aspects: one is feature extraction and the other is pseudorandomization technique. Most hashing schemes combine both aspects to generate an intermediate hash as the first step and then incorporate a compression operation in postprocessing to generate the final hash [1, 10, 11]. Obviously, the robustness and security, two principal properties of hashing, lie in the first step. In order to resist routine unmalicious degradations (e.g., noising, compression) and other malicious attacks (e.g., cropping, rotation), the more invariant features are extracted, the more robust a hash scheme is. However, using features directly makes the scheme susceptible to forgery attacks. Therefore, pseudorandomization techniques should be employed in the hash schemes to assure the security.
Aiming at resisting both routine unmalicious degradations and malicious attacks, various approaches have been proposed in literatures for constructing image hashes, although there is no universallyoptimal hashing approach that is robust against all types of attacks. For example, Radon Soft Hash algorithm (RASH) [12] shows robustness against geometric transformation and some image processing attacks using Radon transform and principle component analysis (PCA). Swaminathan's hashing scheme [8] incorporates pseudorandomization into Fourier-Mellin transform to achieve better robustness to geometric operations. However, it suffers from some classical signal processing operations such as noising. It was also proposed in [9] to generate the hash by detecting invariant feature points, though the expensive searching and removal of feature points by malicious attacks such as cropping and blurring limit its performance in practice. Other content-preserving features based on statistics [1] and spectrum information [2, 13] have also contributed to the development of image hashing and enlightened some novel directions.
Recently, several image hashing schemes based on dimension reduction have been developed and reported to outperform previous techniques. For instance, using low-rank matrix approximations obtained via singular value decomposition (SVD) for hashing was explored in [14]. Its robustness against geometric attacks motivated other solutions in this direction. Monga introduced another dimension reduction technique, called nonnegative matrix factorization (NMF) [15], into their new hashing algorithm [16]. The major benefit of NMF hashing is the structure of the basis resulting from its nonnegative constraints, which lead to a parts-based representation. In contrast to the global representation obtained by SVD, the non-negativity constraints result in a basis of interesting local features [17]. Based on the results in [16], the NMF hashing possesses excellent robustness under a large class of perceptually insignificant attacks, while it significantly reduces misclassification for perceptually distinct images. Note that, for simplicity, we sometimes refer the NMF-NMF-SQ hashing scheme, which was shown to provide the best performance among NMF-based hashing schemes investigated in [16], simply as NMF hashing in this paper.
Inspired by the potential of dimension reduction techniques for image hashing, we introduced Fast Johnson-Lindenstrauss transform (FJLT), a dimension reduction technique recently proposed in [18], into our new robust and secure image hashing algorithm [19]. FJLT shares the low-distortion characteristics of a random projection process but requires a lower computational complexity. It is also more suitable for practical implementation because of its high computational efficiency and security due to the random projection. Since we mainly focus on invariant feature extraction and are interested in image identification applications, the FJLT hashing seems promising because of its robustness to a large class of minor degradations and malicious attacks. Considering the fact that NMF hashing was reported to significantly outperform other existing hashing approaches [16], we use it as the comparison base for the proposed FJLT hashing. Our preliminary experimental results in [19] showed that FJLT hashing provides competitive or even better identification performance under various attacks such as additive noise, blurring, and JPEG compression. Moreover, its lower computational cost also makes it attractive.
However, geometric attacks such as rotation could essentially tamper the original images and thus prevent the accurate identification if we apply the hashing algorithms directly on the manipulated image. Even for the FJLT hashing, it still suffers from the rotation attacks with low identification accuracy. To address this concern, motivated by the work [8, 20], we plan to apply the Fourier-Mellin transform (FMT) on the original images first to make them invariant to geometric transform. Our later experimental results show that, under rotation attacks, the FJLT hashing combined with the proposed FMT preprocessing yields a better identification performance than that of the direct FJLT hashing.
Considering that a specific feature descriptor may be more robust against certain types of attacks, it is desirable to take advantage of different features together to enhance the overall robustness of hashing. Therefore we further propose an extended concept, namely, content-based fingerprinting, to represent a combined, superior hashing approach based on different robust feature descriptors. Similar to the idea of having the unique fingerprint for each human being, we aim at combining invariant characteristics of each feature to construct an exclusive (unique) identifier for each image. Under the framework of content-based fingerprinting, the inputs to the hashing algorithms are not restricted to the original images only, but can also be extendable to include various robust features extracted from the images, such as color, texture, and shape. An efficient joint decision scheme is important for such a combinational framework and significantly affects the identification accuracy. Our experimental results demonstrate that the content-based fingerprinting using a simple joint decision scheme can provide a better performance than the traditional onefold hashing approach. More sophisticated joint decision-making schemes are worth further being investigated in the future.
The rest of this paper is organized as follows. We first introduce the background and theoretic details about FJLT in Section 2. We then describe the proposed hashing algorithm based on random sampling and FJLT in Section 3. In Section 4, we propose the RI-FJLT hashing by combining the Fourier-Mellin transform and FJLT hashing to achieve better geometric robustness. To combine the advantages of both FJLT and RI-FJLT hashing algorithms, a general framework and experimental results of content-based fingerprinting using FJLT hashing for multimedia identification are presented in Section 5. The analytical and experimental results are exhibited in Section 6 to demonstrate the superior performance of the proposed schemes. The conclusion and suggestions for future work are given in Section 7.
2. Theoretical Background
Based on the literature review in Section 1, the current task of image hashing is to extract more robust features to guarantee the identification accuracy under manifold manipulations (e.g., noising, blurring, compression, etc.) and incorporate the pseudorandomization techniques into the feature extraction to enhance the security of the hash generation. According to the information theory [21], if we consider the original image as a source signal, similar to a transmission channel in communication, the feature extraction process will make the loss of information inevitable. Therefore, how to efficiently extract the robust features as lossless as possible is a key issue that the hashing algorithms such as SVD [14], NMF [16], and our FJLT hashing want to tackle.
2.1. Fast Johnson-Lindenstrauss Transform
The Johnson-Lindenstrauss (JL) theorem has found numerous applications, including searching for approximate nearest neighbors (ANNs) [18] and dimension reduction in database, and so forth, by the JL lemma [22],  points in Euclidean space can be projected from the original
points in Euclidean space can be projected from the original  dimensions down to lower
dimensions down to lower  dimensions while just incurring a distortion of at most
dimensions while just incurring a distortion of at most  in their pairwise distances, where
in their pairwise distances, where  . Based on the JL theorem, Alion and Chazelle [18] proposed a new low-distortion embedding of
. Based on the JL theorem, Alion and Chazelle [18] proposed a new low-distortion embedding of  into
into  , called Fast Johnson-Lindenstrauss transform (FJLT). FJLT is based on preconditioning of a sparse projection matrix with a randomized Fourier transform. Note that we will only consider the
, called Fast Johnson-Lindenstrauss transform (FJLT). FJLT is based on preconditioning of a sparse projection matrix with a randomized Fourier transform. Note that we will only consider the  case
case  because our hash is measured by the
because our hash is measured by the  norm. For the
norm. For the  case, interested readers please refer to [18].
case, interested readers please refer to [18].
Briefly speaking, FJLT is a random embedding, denoted as  , that can be obtained as a product of three real-valued matrices:
, that can be obtained as a product of three real-valued matrices:

where the matrices  and
and  are random and
are random and  is deterministic [18].
is deterministic [18].
(i) is a
is a  -by-
-by- matrix whose elements
matrix whose elements  are drawn independently according to the following distribution, where
are drawn independently according to the following distribution, where  means a Normal distribution with zero-mean and variance
means a Normal distribution with zero-mean and variance  ,
,

where

for a large enough constant  .
.
(ii) is a
is a  -by-
-by- normalized Hadamard matrix with the elements as
normalized Hadamard matrix with the elements as

where  is the dot-product of the
is the dot-product of the  -bit vectors of
-bit vectors of  expressed in binary.
expressed in binary.
(iii) is a
is a  -by-
-by- diagonal matrix, where each diagonal element
diagonal matrix, where each diagonal element  is drawn independently from
is drawn independently from  with probability 0.5.
with probability 0.5.
Therefore,  is a
is a  -by-
-by- matrix, where
matrix, where  is the original dimension number of the data and
is the original dimension number of the data and  is the lower dimension number, which is set to be
is the lower dimension number, which is set to be  . Here,
. Here,  is the number of data points,
is the number of data points,  is the distortion rate, and
is the distortion rate, and  is a constant. Given any data point
is a constant. Given any data point  from a
from a  -dimension space, it is intuitively mapped to the data point
-dimension space, it is intuitively mapped to the data point  at a lower
at a lower  -dimension space by the FJLT and the distortion of their pairwise distances could be illustrated by Johnson-Lindenstrauss lemma [18].
-dimension space by the FJLT and the distortion of their pairwise distances could be illustrated by Johnson-Lindenstrauss lemma [18].
2.2. The Fast Johnson-Lindenstrauss Lemma
Lemma 1.
Fix any set  of
of  vectors in
vectors in  ,
,  , and let
, and let  . With probability at least
. With probability at least  , the following two events occur.
, the following two events occur.
() For all  ,
,

() The mapping  requires
requires

operations.
Proofs of the previous theorems can be found in [18]. Note that the probability of being successful (at least  ) arises from the random projection and could be amplified to
) arises from the random projection and could be amplified to  for any
for any  , if we repeat the construction
, if we repeat the construction  times [18]. Since the random projection is actually a pseudorandom process determined by a secret key in our case, most of the keys (at least
times [18]. Since the random projection is actually a pseudorandom process determined by a secret key in our case, most of the keys (at least  ) are satisfied with the distortion bound described in FJLT lemma and could be used in our hashing algorithm. Hence, the FJLT will make our scheme widely applicable for most of the keys and suitable to be applied in practice.
) are satisfied with the distortion bound described in FJLT lemma and could be used in our hashing algorithm. Hence, the FJLT will make our scheme widely applicable for most of the keys and suitable to be applied in practice.
3. Image Hashing via FJLT
Motivated by the hashing approaches based on SVD [14] and NMF [16], we believe that dimension reduction is a significantly important way to capture the essential features that are invariant under many image processing attacks. For FJLT, three benefits facilitate its application in hashing. First, FJLT is a random projection, enhancing the security of the hashing scheme. Second, FJLT's low distortion guarantees its robustness to most routine degradations and malicious attacks. The last one is its low computation cost when implemented in practice. Hence, we propose to use FJLT for our new hashing algorithm. Given an image, the proposed hashing scheme consists of three steps: random sampling, dimension reduction by FJLT, and ordered random weighting. Due to our purpose, we are only interested in feature extraction and randomization. The hash generated by FJLT is just an intermediate hash. For readers who are interested in generating the final hash by compression step, as in the frameworks[8, 9], they are suggested to refer [1, 11] for details.
3.1. Random Sampling
The idea of selecting a few subimages as original feature by random sampling, as shown in Figure 1, is not novel [14, 16]. However, in our approach, we treat each subimage as a point in a high-dimensional space rather than a two-dimensional matrix as in SVD hashing [14] and NMF hashing [16]. For instance, the subimage in Figure 1, which is a  -by-
-by- patch, is actually a point in the
patch, is actually a point in the  -dimensional space in our case, where we focus on gray images.
-dimensional space in our case, where we focus on gray images.
Given an original color image, we first convert it to a gray image and pseudorandomly select  subimages depending on the secret key and get
subimages depending on the secret key and get  , for
, for  . Each
. Each  is a vector with length
is a vector with length  by concatenating the columns of the corresponding subimage. Then we construct our original feature as.
by concatenating the columns of the corresponding subimage. Then we construct our original feature as.

The advantage of forming such a feature is that we can capture the global information in the  matrix and local information in each component
matrix and local information in each component  . Even if we lose some portions of the original image under geometric attacks such as cropping, it will only affect one or a few components in our
. Even if we lose some portions of the original image under geometric attacks such as cropping, it will only affect one or a few components in our  matrix and have no significant influence on the global information. However, the
matrix and have no significant influence on the global information. However, the  matrix with the high dimension (e.g.,
matrix with the high dimension (e.g.,  , when
, when  ) is too large to store and match, which motivates us to employ dimension reduction techniques.
) is too large to store and match, which motivates us to employ dimension reduction techniques.
3.2. Dimension Reduction by FJLT
Based on the theorems in Section 2, FJLT is able to capture the essential features of the original data in a lower-dimensional space with minor distortion, if the factor  is close to 0. Recall the construction
is close to 0. Recall the construction  , our work is to map the
, our work is to map the  matrix from a high-dimensional space to a lower-dimensional space with minor distortion. We first get the three real-valued matrices
matrix from a high-dimensional space to a lower-dimensional space with minor distortion. We first get the three real-valued matrices  ,
,  , and
, and  in our case, which is
in our case, which is  , where
, where  is deterministic but
is deterministic but  and
and  are pseudorandomly dependent on the secret key. The lower dimension
are pseudorandomly dependent on the secret key. The lower dimension  is set to be
is set to be  and
and  is a constant. Then we can get our intermediate hash (
is a constant. Then we can get our intermediate hash ( ) as
) as

Here, the advantage of FJLT is that we can determine the lower dimension  by adjusting the number of data points, which is the number of image blocks by random sampling in our case, and the distortion rate
by adjusting the number of data points, which is the number of image blocks by random sampling in our case, and the distortion rate  . This provides us with a good chance to get a better identification performance. However, the smaller
. This provides us with a good chance to get a better identification performance. However, the smaller  is, the larger
is, the larger  is. Hence we need to make a tradeoff between
is. Hence we need to make a tradeoff between  and
and  in a real implementation.
in a real implementation.
3.3. Ordered Random Weighting
Although the original feature set has been mapped to a lower-dimensional space with a small distortion, the size of intermediate hash can still be large. For instance, if we set  , and
, and  , the size of
, the size of  will be
will be  -by-
-by- . To address this issue, similar to the NMF-NMF-SQ hashing in [16], we can introduce the pseudorandom weight vectors
. To address this issue, similar to the NMF-NMF-SQ hashing in [16], we can introduce the pseudorandom weight vectors  with
with  drawn from the uniform distribution
drawn from the uniform distribution  by the secret key, and we can calculate the final secure hash as
by the secret key, and we can calculate the final secure hash as

where  is the
is the  th column in
th column in  , and
, and  is the inner product of the vectors
is the inner product of the vectors  and
and  . Hence, the final hash is obtained as a vector with length
. Hence, the final hash is obtained as a vector with length  for each image, which is compact and secure. However, the weight vector
for each image, which is compact and secure. However, the weight vector  drawn from
drawn from  could diminish the distance between the hash components
could diminish the distance between the hash components  and
and  from two images and degrade the identification accuracy later. Here we describe a simple example to explain this effect. Suppose we have two vectors
from two images and degrade the identification accuracy later. Here we describe a simple example to explain this effect. Suppose we have two vectors  and
and  , the Euclidean distance is 9. In the first case, if we assign the weight vector
, the Euclidean distance is 9. In the first case, if we assign the weight vector  to
to  and
and  , after the inner product (9), the hash values of
, after the inner product (9), the hash values of  and
and  will be 1.9 and 1, respectively. Obviously, the distance between
will be 1.9 and 1, respectively. Obviously, the distance between  and
and  is significantly shortened. However, if we assign the weight
is significantly shortened. However, if we assign the weight  to
to  and
and  in the second case, after the inner product (9), the hash values of
in the second case, after the inner product (9), the hash values of  and
and  will be 9.1 and 1, respectively. The distance between
will be 9.1 and 1, respectively. The distance between  and
and  is still 8.1. We would like to maintain the distinction of two vectors and avoid the effect of an inappropriate weight vector as the first case.
is still 8.1. We would like to maintain the distinction of two vectors and avoid the effect of an inappropriate weight vector as the first case.
To maintain this distance-preserving property, a possible simple solution, referred as ordered random weighting, is to sort the elements of  and
and  in a descending order before the inner product (9) and make sure that a larger weight value will be assigned to a larger component. In this way, the perceptual quality of the hash vector is retained by minimizing the influence of the weights. To demonstrate the effects of ordering, we investigate the correlation between the intermediate hash distances and the final hash distances when employing the unordered random weighting and ordered random weighting. Intuitively, for both the intermediate hash and the final hash, the distance between the hash generated from the original image (without distortion) and the hash from its distorted copy should increase when the attack/distortion is more severe. One example is illustrated in Figure 2, where we investigate 50 nature images and their 10 distorted copies with Salt and Pepper noise attacks (with variance level:
in a descending order before the inner product (9) and make sure that a larger weight value will be assigned to a larger component. In this way, the perceptual quality of the hash vector is retained by minimizing the influence of the weights. To demonstrate the effects of ordering, we investigate the correlation between the intermediate hash distances and the final hash distances when employing the unordered random weighting and ordered random weighting. Intuitively, for both the intermediate hash and the final hash, the distance between the hash generated from the original image (without distortion) and the hash from its distorted copy should increase when the attack/distortion is more severe. One example is illustrated in Figure 2, where we investigate 50 nature images and their 10 distorted copies with Salt and Pepper noise attacks (with variance level:  ) from our database described in Section 5.1. We observe that the normalized intermediate hash distance and the final hash distance are highly correlated when using ordered random weighting, as shown in Figure 2(a), while the distances are much less correlated under unordered random weighting, as shown in Figure 2(b). In Figure 2, one example of distance correlation based on one of the 50 nature images is indicated by the solid purple lines, where a monotonically increasing relationship between the distances is clearly noticed when using ordered random weighting. Figure 2 suggests that the ordered random weighting in the proposed hashing approach maintains the property of low distortion in pairwise distances of the FJLT dimension reduction technique.
) from our database described in Section 5.1. We observe that the normalized intermediate hash distance and the final hash distance are highly correlated when using ordered random weighting, as shown in Figure 2(a), while the distances are much less correlated under unordered random weighting, as shown in Figure 2(b). In Figure 2, one example of distance correlation based on one of the 50 nature images is indicated by the solid purple lines, where a monotonically increasing relationship between the distances is clearly noticed when using ordered random weighting. Figure 2 suggests that the ordered random weighting in the proposed hashing approach maintains the property of low distortion in pairwise distances of the FJLT dimension reduction technique.
Furthermore, we also investigate the effect of ordering on the identification performance by comparing the ordered and unordered random weighting approaches. One illustrative example is shown in Figure 3, where the distances between different hashes are reported. Among 50 original images, we randomly pick out one as the target image and use its distorted copies as the query images to be identified. To compare the normalized Euclidean distances between the final hashes of the query images and the original 50 images, the final hash distances between the target image and its distorted copies are indicated by red squares, and others are marked by blue crosses. For the Salt and Pepper noise attacks (with variance level:  ) as shown in Figures 3(a) and 3(b), we can see that, when using both ordered random weighting and unordered random weighting, the query images could be easily identified as the true target image based on the identification process described in Section 3.4.1. It is also clear that the ordered random weighting approach should provide a better identification performance statistically since the distance groups are better separated. For the Gaussian blurring attacks (with filter size:
) as shown in Figures 3(a) and 3(b), we can see that, when using both ordered random weighting and unordered random weighting, the query images could be easily identified as the true target image based on the identification process described in Section 3.4.1. It is also clear that the ordered random weighting approach should provide a better identification performance statistically since the distance groups are better separated. For the Gaussian blurring attacks (with filter size:  ) as shown in Figures 3(c) and 3(d), it is clear that the correct classification/identification can only be achieved by using the ordered random weighting. Based on the two examples illustrated in Figure 3 and the tests on other attacks described in Section 6.1, we notice that the identification performance under the blurring attacks is significantly improved using the ordered random weighting when compared with the unordered approach. The improvement is less significant under noise and other attacks. In summary, we observe that ordered random weighting maintains better the distance-preserving property of FJLT compared with the unordered random weighting and thus yields a better identification performance.
) as shown in Figures 3(c) and 3(d), it is clear that the correct classification/identification can only be achieved by using the ordered random weighting. Based on the two examples illustrated in Figure 3 and the tests on other attacks described in Section 6.1, we notice that the identification performance under the blurring attacks is significantly improved using the ordered random weighting when compared with the unordered approach. The improvement is less significant under noise and other attacks. In summary, we observe that ordered random weighting maintains better the distance-preserving property of FJLT compared with the unordered random weighting and thus yields a better identification performance.
Illustrative examples to demonstrate the effect of ordering on the identification performance. The final hash distances between the query images and the original 50 images are shown for comparing the ordered random weighting and the unordered random weighting approaches. (a) and (b) The query images are under Salt and Pepper noise attacks. (c) and (d) The query images are under Gaussian blurring attacks.OrderedUnorderedOrderedUnordered
3.4. Identification and Evaluation
3.4.1. Identification Process
Let  be the set of original images in the tested database and define a space
be the set of original images in the tested database and define a space  as the set of corresponding hash vectors. We use Euclidean distance as the performance metric to measure the discriminating capability between two hash vectors, defined as
as the set of corresponding hash vectors. We use Euclidean distance as the performance metric to measure the discriminating capability between two hash vectors, defined as

where  means the corresponding hash vector with length
means the corresponding hash vector with length  of the image
of the image  . Given a tested image
. Given a tested image  , we first calculate its hash
, we first calculate its hash  and then obtain its distances to each original image in the hash space
and then obtain its distances to each original image in the hash space  . Intuitively, the query image
. Intuitively, the query image  is identified as the
is identified as the  th original images which yields the minimum corresponding distance, expressed as
th original images which yields the minimum corresponding distance, expressed as

The simple identification process described above can be considered as a special case of the  -nearest-neighbor classification approach with
-nearest-neighbor classification approach with  . Here
. Here  is set as 1 since we only have one copy of each original image in the current database. For a more general case, if we have
is set as 1 since we only have one copy of each original image in the current database. For a more general case, if we have  multiple copies of each original image with no distortion or with only slight distortions, we could adopt the
multiple copies of each original image with no distortion or with only slight distortions, we could adopt the  -nearest neighbor (KNN) algorithm for image identification in our problem.
-nearest neighbor (KNN) algorithm for image identification in our problem.
3.4.2. Receiver Operating Characteristics Analysis
Except investigating identification accuracy, we also study the receiver operating characteristics (ROC) curve [23] to visualize the performance of different hashing approaches, including NMF-NMF-SQ hashing, FJLT hashing, and Content-based fingerprinting proposed later. The ROC curve depicts the relative tradeoffs between benefits and cost of the identification and is an effective way to compare the performances of different hashing approaches.
To obtain ROC curves to analyze the hashing algorithms, we may define the probability of true identification  and probability of false alarm
and probability of false alarm  as
as

where  is the identification threshold. The images
is the identification threshold. The images  and
and  are two distinct original images and the images
are two distinct original images and the images  and
and  are manipulated versions of the image
are manipulated versions of the image  and
and  , respectively. Ideally, we hope that the hashes of the original image
, respectively. Ideally, we hope that the hashes of the original image  and its manipulated version
and its manipulated version  should be similar and thus be identified accurately, while the distinct images
should be similar and thus be identified accurately, while the distinct images  and
and  should have different hashes. In other words, given a certain threshold
should have different hashes. In other words, given a certain threshold  , an efficient hashing should provide a higher
, an efficient hashing should provide a higher  with a lower
with a lower  simultaneously. Consequently, when we obtain all the distances between manipulated images and original images, we could generate a ROC curve by sweeping the threshold
simultaneously. Consequently, when we obtain all the distances between manipulated images and original images, we could generate a ROC curve by sweeping the threshold  from the minimum value to the maximum value, and further compare the performances of different hashing approaches.
from the minimum value to the maximum value, and further compare the performances of different hashing approaches.
4. Rotation Invariant FJLT Hashing
Although the Fast Johnson-Lindenstrauss transform has been shown to be successful in the hashing in our previous preliminary work [19], the FJLT hashing can still be vulnerable to rotation attacks. Based on the hashing scheme described in Section 3, random sampling can be an effective approach to reduce the distortion introduced by cropping, and scaling attack can be efficiently tackled by upsampling and downsampling in the preprocessing. However, to successfully handle the rotation attacks, we need to introduce other geometrically invariant transform to improve the performance of the original FJLT hashing.
4.1. Fourier-Mellin Transform
The Fourier-Mellin transform (FMT) is a useful mathematical tool for image recognition and registration, because its resulting spectrum is invariant to rotation, translation, and scaling [8, 20]. Let  denote a gray-level image defined over a compact set of
denote a gray-level image defined over a compact set of  , the standard FMT of
, the standard FMT of  in polar coordinates (log-polar coordinates) is given by
in polar coordinates (log-polar coordinates) is given by

If we make  , (13) is clearly a Fourier transform like
, (13) is clearly a Fourier transform like

Therefore, the FMT could be divided into three steps, which result in the invariance to geometric attacks.
(i)Fourier Transform. It converts the translation of original image in spatial domain into the offset of angle in spectrum domain. The magnitude is translation invariant.
(ii)Cartesian to Log-Polar Coordinates. It converts the scaling and rotation in Cartesian coordinates into the vertical and horizontal offsets in Log-Polar Coordinates.
(iii)Mellin Transform. It is another Fourier transform in Log-Polar coordinates and converts the vertical and horizontal offsets into the offsets of angles in spectrum domain. The final magnitude is invariant to translation, rotation, and scaling.
However, the inherent drawback of the Fourier transform makes FMT only robust to geometric transform, but vulnerable to many other classical signal processing distortions such as cropping and noising. As we know, when converting an image into the spectrum domain by 2D Fourier transform, each coefficient is contributed by all the pixels of the image. It means that the Fourier coefficients are dependent on the global information of the image in the spatial domain. Therefore, the features extracted by Fourier-Mellin transform are sensitive to certain attacks such as noising and cropping, because the global information is no longer maintained. To overcome this problem, we have modified the FMT implementation in our proposed rotation-invariant FJLT (RI-FJLT) hashing.
4.2. RI-FJLT Hashing
The invariance of FMT to geometric attacks such as rotation and scaling has been widely applied in image hashing [3, 8] and watermarking [20, 24]. It also motivates us to address the deficiency of FJLT hashing by incorporating FMT. Here, we propose the rotation-invariant FJLT hashing by introducing FMT into the FJLT hashing. Specially, the proposed rotation-invariant FJLT hashing (RI-FJLT) consists of three steps.
Step 1.
Converting the image into the Log-Polar coordinates

where  and
and  are Cartesian coordinates and
are Cartesian coordinates and  and
and  are Log-Polar coordinates. Any rotation and scaling will be considered as vertical and horizontal offsets in Log-Polar coordinates. An example is given in Figure 4.
are Log-Polar coordinates. Any rotation and scaling will be considered as vertical and horizontal offsets in Log-Polar coordinates. An example is given in Figure 4.
Step 2.
Applying Mellin transform (Fourier transform under Log-Polar coordinates) to the converted image and return the magnitude feature image.
Step 3.
Applying FJLT hashing in Section 3 to the magnitude feature image derived in Step 2.
For the conversion in Step 1, since the pixels in Cartesian coordinates are not able to be one-to-one mapped to pixels in the Log-Polar coordinates space, some value interpolation approaches are needed. We have investigated three different interpolation approaches for the proposed RI-FJLT hashing, including nearest neighbor, bilinear and bicubic interpolations, and found that the bilinear is superior to others. Therefore we only report the results under bilinear interpolation here. Note that we abandon the first step of FMT in RI-FJLT hashing, because we only focus on rotation attacks (other translations are considered as cropping) and it is helpful to reduce the influence of noising attacks by removing the Fourier transform step. The performance will be illustrated in Section 6. However, since Step 2 can inevitably be affected by attacks such as noising, some preprocessing such as median filtering can help improve the final identification performance.
5. Content-Based Fingerprinting
5.1. Concept and Framework
Considering that certain features can be more robust against certain attacks, to take advantage of different features, we plan to propose a new content-based fingerprinting concept. This concept combines benefits of conventional content-based indexing (used to extract discriminative content features) and multimedia hashing. Here we define content-based image fingerprinting as a combination of multiple robust feature descriptors and secure hashing algorithms. Similar to the concept of image hash, it is a digital signature based on the significant content of image itself and represents a compact and discriminative description for the corresponding image. Therefore, it has a wide range of applications in practice such as integrity verification, watermarking, content-based indexing, identification, and retrieval. The framework is illustrated in Figure 5.
Specially, each vertical arrow in Figure 5 represents an independent hashing generation procedure, which consists of robust feature extraction and intermediate hash generation proposed by [8, 10]. Because it is the combination of various hash descriptors, the content-based fingerprinting can be considered as an extension and evolution of image hashing and thus offers much more freedom to accommodate different robust features (color, shape, texture, salient points, etc., [7]) and design efficient hashing algorithms to successfully against different types of attacks and distortions. Similar to the idea of finding one-to-one relationships between the fingerprints and an individual human being, the goal of content-based fingerprinting is to generate an exclusive digital signature, which is able to uniquely identify the corresponding media data no matter which content-preserving manipulation or attack is taken on.
Compared with the traditional image hashing concept, the superiority of content-based fingerprint concept lies in its potential high discriminating capability, better robustness, and multilayer security arising from the combination of various robust feature descriptors and a joint decision-making process. Same as in any information fusion processes, theoretically the discrimination capability of the content-based fingerprinting with effective joint decision-making scheme should outperform a single image hashing. Since the content-based fingerprint consists of several hash vectors, which are generated based on various robust features and different secret keys, it is argued that the framework of content-based fingerprinting results in a better robustness and multilayer security when an efficient joint decision-making is available. However, combining multiple image hashes approaches requires additional computation cost for the generation of content-based fingerprinting. The tradeoff between computation cost and performance is a concern with great importance in practice.
5.2. A Simple Content-Based Fingerprinting Approach
From the experimental results in Section 6, we note that FJLT hashing is robust to most types of the tested distortions and attacks except for rotation attacks and that RI-FJLT hashing provides a significantly better performance for rotation attacks at the cost of the degraded performances under other types of attacks. Recall an important fact that it is relatively easy to find a robust feature to resist one specific type of distortion; however it is very difficult, if not impossible, to find a feature which is uniformly robust to against all types of distortions and attacks. Any desire to generate an exclusive signature for the image by a single image hashing approach is infeasible. Here we plan to demonstrate the advantages of the concept of content-based fingerprinting by combining the proposed FJLT hashing and RI-FJLT hashing. The major components of the content-based fingerprinting framework include hash generations and the joint decision-making process which should take advantage of the combinations of the hashes to achieve a superior identification decision-making. Regarding the joint decision-making, there are many approaches in machine learning [25] that can be useful. Here we only present a simple decision-making process in rank level [26] to demonstrate the superiority of content-based fingerprinting.
Given an image  with certain distortion, we, respectively, generate the hash vectors
with certain distortion, we, respectively, generate the hash vectors  and
and  by FJLT and RI-FJLT hashing. Suppose that the hash values of original images
by FJLT and RI-FJLT hashing. Suppose that the hash values of original images  are
are  and
and  generated by FJLT and RI-FJLT hashing, respectively. We denote
generated by FJLT and RI-FJLT hashing, respectively. We denote  as the confidence measure that we identify image
as the confidence measure that we identify image  as image
as image  when applying the FJLT hashing. Similarly,
when applying the FJLT hashing. Similarly,  is denoted for that of the RI-FJLT hashing. Here, we simply define
is denoted for that of the RI-FJLT hashing. Here, we simply define

where  and
and  are preselected weights in the case of FJLT and RI-FJLT hashing, respectively, and
are preselected weights in the case of FJLT and RI-FJLT hashing, respectively, and  means the Euclidean norm. Considering the poor performances of RI-FJLT hashing under many other types of attacks except for rotation ones, we intuitively introduce a weight
means the Euclidean norm. Considering the poor performances of RI-FJLT hashing under many other types of attacks except for rotation ones, we intuitively introduce a weight  , where
, where  , to the original confidence measures of FJLT and RI-FJLT hashing to decrease the possible negative influence of RI-FJLT hashing and maintain the advantages of both FJLT and RI-FJLT hashing in the proposed content-based fingerprinting under different attacks.
, to the original confidence measures of FJLT and RI-FJLT hashing to decrease the possible negative influence of RI-FJLT hashing and maintain the advantages of both FJLT and RI-FJLT hashing in the proposed content-based fingerprinting under different attacks.
Regarding the identification decision making, given a tested image  , we calculate all the confidence measures
, we calculate all the confidence measures  and
and  over the image database of
over the image database of  by using FJLT and RI-FJLT hashing, and make the identification decision correspondingly by selecting the highest one among
by using FJLT and RI-FJLT hashing, and make the identification decision correspondingly by selecting the highest one among  and
and  . Note that if a confidence measure
. Note that if a confidence measure  is negative, it means that the image
is negative, it means that the image  is outside the confidence interval of the image
is outside the confidence interval of the image  and the confidence measure is assigned to be zero.
and the confidence measure is assigned to be zero.
6. Analytical and Experimental Results
6.1. Database and Content-Preserving Manipulations
In order to evaluate the performance of the proposed new hashing algorithms, we test FJLT hashing and RI-FJLT hashing on a database of 100 000 images. In this database, there are 1000 original color nature images, which are mainly selected from the ten sets of categories in the content-based image retrieval database of the University of Washington (http://www.cs.washington.edu/research/imagedatabase/) as well as our own database. Therefore, some of the original images can be similar in content if they come from the same category, and some are distinct if they come from the different categories. For each original color image with size  , we generate 99 similar but distorted versions by manipulating the original image according to eleven classes of content-preserving operations, including additive noise, filtering operations, and geometric attacks, as listed in Table 1. All the operations are implemented using Matlab. Here we give some brief explanations of some ambiguous manipulations. For image rotation, a black frame around the image will be added by Matlab but some parts of image will be cut if we want to keep its size the same as the original image. An example is given in Figure 4(b). Here our cropping attacks refer to the removal of the outer parts (i.e., let the values of the pixels on each boundary be equal to null and keep the significant content in the middle).
, we generate 99 similar but distorted versions by manipulating the original image according to eleven classes of content-preserving operations, including additive noise, filtering operations, and geometric attacks, as listed in Table 1. All the operations are implemented using Matlab. Here we give some brief explanations of some ambiguous manipulations. For image rotation, a black frame around the image will be added by Matlab but some parts of image will be cut if we want to keep its size the same as the original image. An example is given in Figure 4(b). Here our cropping attacks refer to the removal of the outer parts (i.e., let the values of the pixels on each boundary be equal to null and keep the significant content in the middle).
6.2. Identification Results and ROC Analysis
Our preliminary study [19] on a small database showed that FJLT hashing provides nearly perfect identification accuracy for the standard test images such as Baboon, Lena, and Peppers. Here we will measure the FJLT hashing and the new proposed RI-FJLT hashing on the new database, which consists of 1000 nature images from ten categories. Ideally, to be robust to all routine degradations and malicious attacks, no matter what content-preserving manipulation is done, the image with any distortion should still be correctly classified into the corresponding original image.
It is worth mentioning that all the pseudorandomizations of NMF-NMF-SQ hashing, FJLT hashing, and content-based fingerprinting are dependent on the same secret key in our experiment. As discussed in [16], the secret keys, more precisely the key-based randomizations, play important roles on both increasing the security (i.e., making the hash unpredictable) and enhancing scalability (i.e., keeping the collision ability from distinct images low and thus yielding a better identification performance) of the hashing algorithm. Therefore, the identification accuracy of a hashing algorithm is determined simultaneously by both the dimension reduction techniques (e.g., FJLT and NMF) and the secret keys. As shown in NMF hashing in [16], if we generate hashes of different images with varied secret keys, the identification performance can be further improved significantly because the secret key boosts up the cardinality of the probability space and brings down the probability of false alarm. In this paper, because we mainly focus on examining the identification capacity of hashing schemes themselves rather than the effects of secret keys, to minimize the effects of the factor of the secret keys, we use the same key in generating hash vectors for different images.
6.2.1. Results of FJLT Hashing
Following the algorithms designed in Section 3, we test the FJLT hashing with the parameters chosen as  ,
,  ,
,  ,
,  , as summarized in Table 3. Note that most of the keys could be used in FJLT hashing because of its robustness to secret keys, which has been illustrated in [19]. Since the NMF-NMF-SQ hashing has been shown to outperform the SVD-SVD and PR-SQ hashing algorithms having the best known robustness properties in the existing literature, we compare the performance of our proposed FJLT hashing algorithm with NMF-NMF-SQ hashing when testing on the new database. For the NMF approach, the parameters are set as
, as summarized in Table 3. Note that most of the keys could be used in FJLT hashing because of its robustness to secret keys, which has been illustrated in [19]. Since the NMF-NMF-SQ hashing has been shown to outperform the SVD-SVD and PR-SQ hashing algorithms having the best known robustness properties in the existing literature, we compare the performance of our proposed FJLT hashing algorithm with NMF-NMF-SQ hashing when testing on the new database. For the NMF approach, the parameters are set as  ,
,  ,
,  ,
,  , and
, and  according to [16]. It is worth mentioning that, to be consistent with the FJLT approach, we chose the same size of subimages and length of hash vector in NMF hashing (denoted as
according to [16]. It is worth mentioning that, to be consistent with the FJLT approach, we chose the same size of subimages and length of hash vector in NMF hashing (denoted as  and
and  ), which facilitate a fair comparison between them later. We also tried the setting
), which facilitate a fair comparison between them later. We also tried the setting  (with
(with  represents the number of subimages in the NMF approach), but it was found that the choice of
represents the number of subimages in the NMF approach), but it was found that the choice of  yields a better performance. Consequently, NMF hash vector has the same length 40 as the FJLT hash vector. We first examine the identification accuracy of both hashing algorithms under different attacks, and the identification results are shown in Table 2. It is clearly noted that the proposed FJLT hashing consistently yields a higher identification accuracy than that of NMF hashing under different types of tested manipulations and attacks.
yields a better performance. Consequently, NMF hash vector has the same length 40 as the FJLT hash vector. We first examine the identification accuracy of both hashing algorithms under different attacks, and the identification results are shown in Table 2. It is clearly noted that the proposed FJLT hashing consistently yields a higher identification accuracy than that of NMF hashing under different types of tested manipulations and attacks.
We then present a statistical comparison of the proposed FJLT and NMF hashing algorithms by studying the corresponding ROC curves. We first generate the overall ROC curves for all types of tested manipulations when applying different hashing schemes, and the resulting ROC curves are shown in Figure 6. From Figure 6, one major observation is that the proposed FJLT hashing outperforms NMF-NMF-SQ hashing. To test the robustness to each type of attacks, a ROC curve is also generated for a particular attack and hash algorithm. Since we note from Table 2 that the proposed FJLT hashing significantly outperforms NMF-NMF-SQ for additive noise, cropping and gamma correction attacks, we show the ROC curves corresponding to the six attacks (i.e., Gaussian noise, Salt and Pepper noise, Speckle noise, Rotation attacks, Cropping and Gamma correction) in Figure 7. Once again, the ROC curves in Figure 7 reinforce the observation that FJLT hashing significantly outperform the state-of-art NMF hashing. However, both of them are still a little sensitive to Gaussian noise as shown in Figure 7(a). The underlying reason is that we did not incorporate any preprocessing such as median filter into FJLT hashing or NMF hashing, because we would investigate the robustness of FJLT and NMF hashing themselves to additive noise. In practice, the preprocessing such as image denoising before applying image hashing could further improve the robustness to additive noise (referring to the annotation below Table 2), since both FJLT hashing and NMF hashing are strongly robust to blurring. As for the attacks such as JPEG compression and Blurring, since we observe perfect identification performances and no false alarms in our own experiments, we do not report the ROC curves further, which are similar to the ROC results via NMF hashing shown in [16].
The ROC curves of NMF-NMF-SQ hashing, FJLT hashing, and content-based fingerprinting under six types of attacks, respectively. (a) Gaussian noise; (b) Speckle noise; (c) Salt and Pepper noise; (d) Rotation attacks; (e) Cropping; (f) Gamma correction.ROC curves under Gaussian noiseROC curves under Speckle noiseROC curves under Salt and Pepper noiseROC curves under Rotation attacksROC curves under CroppingROC curves under Gamma correction
Here we try to give some intuitive explanations regarding the observed performances of the two hashing algorithms. In NMF hashing, the dimension reduction technique is based on the approximative nonnegative matrix factorization, which factorizes the image matrix into two lower rank matrices. However, the problem of choosing a low rank  (e.g.,
(e.g.,  ,
,  in the NMF hashing) is of great importance, though it is observed to be sensitive to the data. While for FJLT hashing, the mapping is obtained by a coefficients matrix and a subimage is treated as a point in a high-dimensional space (in our case, the dimension is
in the NMF hashing) is of great importance, though it is observed to be sensitive to the data. While for FJLT hashing, the mapping is obtained by a coefficients matrix and a subimage is treated as a point in a high-dimensional space (in our case, the dimension is  ). One advantage of FJLT hashing is that minor modifications in the content will not affect the integrity of the global information, which results in a better performance. However, as illustrated in Table 2 and the ROC curve in Figure 7(d), both FJLT hashing and NMF hashing provide poor performances under rotation attacks, and we shall investigate this problem further.
). One advantage of FJLT hashing is that minor modifications in the content will not affect the integrity of the global information, which results in a better performance. However, as illustrated in Table 2 and the ROC curve in Figure 7(d), both FJLT hashing and NMF hashing provide poor performances under rotation attacks, and we shall investigate this problem further.
6.2.2. Results of RI-FJLT Hashing
In Table 2, we note that one drawback of FJLT hashing is its vulnerability to rotation attacks. Especially, as shown by an example in Figure 4, for a large rotation degree of 45, FJLT hashing failed to identify the image content. Here we apply the RI-FJLT hashing approach presented in Section 6 to overcome this drawback.
We generated 36 rotated versions for each test image in the database and the rotation degrees are varied from 5 to 180 with an interval of 5 degrees. Though not investigated further here, it is worth mentioning that, before the conversion from Cartesian coordinates to Log-Polar coordinates, some preprocessing operations such as median filtering can be helpful to enhance the identification performance [8], especially under additive noise distortions. We have employed median filter as preprocessing in RI-FJLT hashing. The identification results under rotation attacks are shown in Table 4. We can see from the table that FJLT hashing is obviously sensitive to rotation attacks and thus its identification accuracy greatly degrades with the increase of rotation degree. It is also noted that RI-FJLT hashing still consistently achieves almost perfect identification accuracy under rotation attacks even with large rotation degrees.
Although the invariance of Fourier-Mellin transform benefits the FJLT hashing with the robustness to rotation attacks, such robustness to rotation comes at the cost of degraded identification accuracy for other types of manipulations and attacks. We have intuitively discussed the reasons for this observation in Section 4. We argue that it may not be feasible to be robustly against various attacks by only depending on single feature descriptor. This observation motivates us to look for an alternative solution that is the content-based fingerprinting we proposed in Section 5 to tackle this problem.
6.2.3. Results of Content-Based Fingerprinting
Since FJLT hashing is demonstrated to be robust against a large class of distortions except for rotation attacks and RI-FJLT hashing achieves superior performance under rotation attacks at the cost of sensitivity to other manipulations, it accounts for the fact that it is very difficult to design a globally optimal hashing approach that could handle all of the distortions and manipulations. Hence, we combine FJLT hashing and RI-FJLT hashing following the framework of content-based fingerprinting proposed in Section 5 and test its performance on the database described in Section 6.1. Considering the poor performance of RI-FJLT hashing on other manipulations, we need to introduce an elaborate weight shown in Section 5.2 to the confidence measure of RI-FJLT hashing to get rid of its negative influence and try to maintain the advantages of both FJLT and RI-FJLT hashing in the proposed content-based fingerprinting. Based on our preliminary study, we set  to keep the advantages of FJLT hashing and find that a good weight
to keep the advantages of FJLT hashing and find that a good weight  could be drawn from the interval range
could be drawn from the interval range  . We set
. We set  in our implementation and exhibit the results in Table 2.
in our implementation and exhibit the results in Table 2.
To have a fair comparison between different approaches, though we combine the FJLT hashing and the RI-FJLT hashing in the content-based fingerprinting, the length of the overall fingerprint vector is still chosen as 40 (with 20 components from the FJLT hashing and the left 20 from the RI-FJLT hashing), which is the same as that of the FJLT hashing and the NMF hashing. It is clear that the simple joint decisionmaking complements the drawback of FJLT hashing under rotation attacks by incorporating the RI-FJLT hashing into the proposed content-based fingerprinting. The ROC curves for FJLT hashing, NMF hashing, and the proposed content-based fingerprinting under rotation attacks are shown in Figure 7(d). Obviously, among the three approaches, the content-based fingerprinting yields the highest true positive rates when the same false positive rates are considered. The ROC curves of the content-based fingerprinting approach under other types of attacks are also illustrated in Figure 7. We note that the robustness of content-based fingerprinting to additive noise, cropping, and Gamma correction slightly degrades, as shown in Figure 7. One possible explanation could be that the current simple decision-making process is not the theoretically optimal one that could eliminate the negative effect of RI-FJLT hashing under these attacks. However, the overall performance of content-based fingerprinting as illustrated by the ROC curve in Figure 6 demonstrates that it is superior and more flexible than a single hashing approach, because the selection of features and secure hashes can be adapted to address different practical application concerns. Therefore, the proposed content-based fingerprinting can be a promising extension and evolution of traditional image hashing.
6.3. Unpredictability Analysis
Except for the robustness against different types of attacks, the security in terms of unpredictability that arises from the key-dependent randomization is another important property of hashing and the proposed content-based fingerprinting. Here we mainly focus on the unpredictability analysis of FJLT hashing, because the unpredictability of the RI-FJLT hashing and the content-based fingerprinting proposed arise from the FJLT hashing. Higher amount of the randomness in the hash values makes it harder for the adversary to estimate and forge the hash without knowing the secret keys. Since it is believed that a high differential entropy is a necessary property of secure image hashes, we evaluate the security in terms of unpredictability of FJLT hashing by quantifying the differential entropy of the FJLT hash vector, as proposed in [8]. The differential entropy of a continuous random variable  is given by
is given by

where  means the probability density function (pdf) of
means the probability density function (pdf) of  and
and  means the support area of
means the support area of  . Since the analytical model of the pdf of the FJLT hash vector component is generally not available, we carry out the practical pdf approximation using the histograms of the hash vector components. Figure 8(a) shows the histogram of a typical component from the FJLT hash vector of image Lena resulting from 3000 different keys. It is noted that it approximately follows a Gaussian distribution. Similarly, we can obtain the histograms of other components. Based on our observations, we state that the FJLT hash vector approximately follows a multivariate Gaussian distribution. Therefore, similar to the hash in [16], we have the differential entropy of the FJLT hash vector
. Since the analytical model of the pdf of the FJLT hash vector component is generally not available, we carry out the practical pdf approximation using the histograms of the hash vector components. Figure 8(a) shows the histogram of a typical component from the FJLT hash vector of image Lena resulting from 3000 different keys. It is noted that it approximately follows a Gaussian distribution. Similarly, we can obtain the histograms of other components. Based on our observations, we state that the FJLT hash vector approximately follows a multivariate Gaussian distribution. Therefore, similar to the hash in [16], we have the differential entropy of the FJLT hash vector  as
as

where  means the determinant of the covariance matrix of the hash vector, and
means the determinant of the covariance matrix of the hash vector, and  means the length of the FJLT hash vector.
means the length of the FJLT hash vector.
From Figure 8(b) where an example of the covariance matrix of the FJLT hash vector is shown, we can see that the covariance matrix is approximately a diagonal matrix, meaning that the components are approximately statistically independent. Therefore,  can be approximately estimated as
can be approximately estimated as

where  means the variance of the component
means the variance of the component  in the FJLT hash vector. Since from information theory, the differential entropy of a random vector
in the FJLT hash vector. Since from information theory, the differential entropy of a random vector  is maximized when
is maximized when  follows a multivariate normal distribution
follows a multivariate normal distribution  [21], we argue that the proposed FJLT hashing is highly secure (unpredictable) as it approximately follows [18]. We note that NMF-NMF-SQ hashing also was shown to approximately follow a joint Gaussian distribution and a similar statement in terms of differential entropy was given in [16]. Hence, we state that the proposed FJLT hash is comparably as secure as NMF hashing, which was shown to be presumably more secure than previously proposed schemes that are based on random rectangles alone [16].
[21], we argue that the proposed FJLT hashing is highly secure (unpredictable) as it approximately follows [18]. We note that NMF-NMF-SQ hashing also was shown to approximately follow a joint Gaussian distribution and a similar statement in terms of differential entropy was given in [16]. Hence, we state that the proposed FJLT hash is comparably as secure as NMF hashing, which was shown to be presumably more secure than previously proposed schemes that are based on random rectangles alone [16].
However, the security of image hashing does not only lie on a higher differential entropy, which is only one aspect of a secure image hashing [8, 16], but also includes other factors such as key diversity and prior knowledge possessed by adversaries. Therefore, how to comprehensively evaluate the security of image hashing is still an open question. Interested readers could refer to the literatures [8, 27] regarding the security analysis issues.
6.4. Computational Complexity
We analyze the computational complexity of the proposed FJLT hashing and RI-FJLT algorithms (the computational cost of content-based fingerprinting is the sum of FJLT and RI-FJLT hashing) when compared with the NMF-NMF-SQ hashing algorithm.
-
(i)
NMF. In [16], the computational complexity of NMF-NMF-SQ hashing has been given as follows. It does a rank
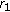 NMF on
NMF on 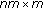 matrices and then a rank
matrices and then a rank 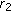 approximation from the resulting
approximation from the resulting  matrix in [16]. At last, pseudorandom numbers are incorporated in the NMF-NMF vector of length
matrix in [16]. At last, pseudorandom numbers are incorporated in the NMF-NMF vector of length 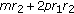 , and the total computation cost is
, and the total computation cost is

-
(ii)
FJLT. Based on the analysis in [18], given a
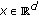 , the computation cost of FJLT on
, the computation cost of FJLT on  is calculated as follows. Computing
is calculated as follows. Computing  requires
requires  time and
time and 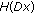 requires
requires 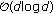 . For computing
. For computing 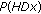 , it takes
, it takes 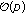 , where the
, where the  is the number of nonzeros in
is the number of nonzeros in 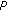 , we know that the
, we know that the 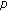 satisfies the Binomial distribution
satisfies the Binomial distribution  , therefore we take the mean value of
, therefore we take the mean value of 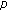 as
as 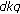 that equals
that equals 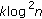 , where
, where 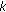 is
is 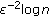 . Then, take the random weight incorporation into account, we have the total computation cost of the FJLT hashing as (
. Then, take the random weight incorporation into account, we have the total computation cost of the FJLT hashing as (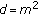 in our case)
in our case)

-
(iii)
RI-FJLT. Except for the cost of FJLT hashing, we need to take the bilinear interpolation that requires
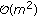 and Fourier transform that takes
and Fourier transform that takes  by FFT into account. Consequently, the cost of RI-FJLT is
by FFT into account. Consequently, the cost of RI-FJLT is

Here, we specify that  in our case and also take other parameters into account. Obviously the FJLT and RI-FJLT hashing roughly require a lower computational cost than that of NMF-NMF-SQ. To have an intuitive feeling of the computational costs required by different algorithms, we also test on a standard image Lena with size
in our case and also take other parameters into account. Obviously the FJLT and RI-FJLT hashing roughly require a lower computational cost than that of NMF-NMF-SQ. To have an intuitive feeling of the computational costs required by different algorithms, we also test on a standard image Lena with size  by using a computer with Intel Core 2 CPU (2.00 GHz) and 2 G RAM. The required computational time is listed in Table 5, which shows that the FJLT and RI-FJLT hashing are much faster than NMF-NMF-SQ hashing. Note that the costs are based on a length 20 of the hash vectors in our experiments. Increasing the length of hash vectors will enhance the identification accuracy but will require more computational costs. This trade-off will be further studied in the future.
by using a computer with Intel Core 2 CPU (2.00 GHz) and 2 G RAM. The required computational time is listed in Table 5, which shows that the FJLT and RI-FJLT hashing are much faster than NMF-NMF-SQ hashing. Note that the costs are based on a length 20 of the hash vectors in our experiments. Increasing the length of hash vectors will enhance the identification accuracy but will require more computational costs. This trade-off will be further studied in the future.
 by FJLT, RI-FJLT and NMF-NMF-SQ hashing algorithms.
by FJLT, RI-FJLT and NMF-NMF-SQ hashing algorithms.7. Discussions and Conclusion
In this paper, we have introduced a new dimension reduction technique—FJLT, and applied it to develop new image hashing algorithms. Based on our experimental results, it is noted that the FJLT-based hashing is robust to a large class of routine distortions and malicious manipulations. Compared with the NMF-based approach, the proposed FJLT hashing can achieve comparable, sometimes better, performances than that of NMF, while requiring less computational cost. The random projection and low distortion properties of FJLT make it more suitable for hashing in practice than the NMF approach. Further, we have incorporated Fourier-Mellin transform to complement the deficiency of FJLT hashing under rotation attacks. The experimental results confirm the fact that generating a hash descriptor based on a ceratin type of features to resist all types of attacks is highly unlikely in practice. However, for a particular type of distortion, it is feasible to find a specific feature to tackle it and obtain good performance. These observations motivate us to propose the concept of content-based fingerprinting as an extension of image hashing and demonstrate the superiority of combining different features and hashing algorithms.
We note that the content-based fingerprinting approach by using FJLT and RI-FJLT still suffers from some distortions, such as Gaussian noise and Gamma correction. One solution is to further find other features that are robust to these attacks/manipulations and incorporate them into the proposed scheme to enhance the performance. Future work will include how to incorporate other robust features (such as the popular SIFT-based features) and secure hashing algorithms to optimize the content-based fingerprinting framework and at the same time explore efficient hierarchical decision-making schemes for identification.
Furthermore, we plan to explore the variations of the current FJLT hashing. Similar to the NMF-based hashing approach (referred as NMF-NMF-SQ hashing in [16]) where the hash is based on a two-stage application of NMF, we can modify the proposed FJLT hashing into a two-stage FJLT-based hashing approach by introducing a second stage of FJLT as follows. Treat the intermediate hash  as a vector with length
as a vector with length  , and then reapply FJLT to obtain a representation of the vector
, and then reapply FJLT to obtain a representation of the vector  with further dimension reduction. Compared with our current one-stage FJLT-based hashing, the length of intermediate hash
with further dimension reduction. Compared with our current one-stage FJLT-based hashing, the length of intermediate hash  could be further shortened by the second FJLT and the security would be enhanced in the two-stage FJLT hashing. However, the robustness of a two-stage FJLT-based hashing under attacks such as cropping may degrade, since now each component in the modified hash vector is contributed by all the subimages by random sampling. Therefore, the distortion of local information in one subimage could affect the whole hash vector rather than a couple of hash components. The computation cost can also be a concern. We will investigate these issues in the future work.
could be further shortened by the second FJLT and the security would be enhanced in the two-stage FJLT hashing. However, the robustness of a two-stage FJLT-based hashing under attacks such as cropping may degrade, since now each component in the modified hash vector is contributed by all the subimages by random sampling. Therefore, the distortion of local information in one subimage could affect the whole hash vector rather than a couple of hash components. The computation cost can also be a concern. We will investigate these issues in the future work.
Another concern that is of great importance in practice but is rarely discussed in the context of image hashing is automation. Automatic estimation/choice of design parameters removes the subjectivity from the design procedure and can yield better performances. For instance, algorithms for automating the design process of image watermarking have already been implemented in the literature [28–30]. However, to our knowledge, this automated solution has not yet been explored in the context of image hashing. Our preliminary study in [31] demonstrated that using a genetic algorithm (GA) for automatic estimation of parameters of the FJLT hashing using could improve the identification performance. However, choosing the appropriate fitness function is challenging in automated image hash. We plan to investigate different fitness functions and how the GA algorithm can incorporate other factors (such as keys) and other constraints (such as the hash length).
References
Venkatesan R, Koon S-M, Jakubowski MH, Moulin P: Robust image hashing. Proceedings of the International Conference on Image Processing (ICIP '00), September 2000, Vancouver, Canada 3: 664-666.
Fridrich J, Goljan M: Robust hash functions for digital watermarking. Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC '00), March 2000, Las Vegas, Nev, USA 178-183.
Wu M, Mao Y, Swaminathan A: A signal processing and randomization perspective of robust and secure image hashing. Proceedings of the IEEE/SP 14th Workshop on Statistical Signal Processing, August 2007, Madison, Wis, USA 166-170.
Wu CW: On the design of content-based multimedia authentication systems. IEEE Transactions on Multimedia 2002, 4(3):385-393. 10.1109/TMM.2002.802018
Martinen E, Wornell GW: Multimedia content authentication: fundamental limits. Proceedings of the IEEE International Conference Image Processing (ICIP '02), 2002, Rochester, NY, USA 2: 17-20.
Lew M, Sebe N, Djeraba C, Jain R: Content-based multimedia information retrieval: state of the art and challenges. ACM Transactions on Multimedia Computing, Communications and Applications 2006, 2(1):1-19. 10.1145/1126004.1126005
Smeulders A, Worring M, Santini S, Gupta A, Jain R: Contentbased image retrieval at the end of the early years. IEEE Transactions on Pattern Analysis and Machine Intelligence 2000, 1349-1380. 10.1109/34.895972
Swaminathan A, Mao Y, Wu M: Robust and secure image hashing. IEEE Transactions on Information Forensics and Security 2006, 1(2):215-230. 10.1109/TIFS.2006.873601
Monga V, Evans BL: Perceptual image hashing via feature points: performance evaluation and tradeoffs. IEEE Transactions on Image Processing 2006, 15(11):3453-3466. 10.1109/TIP.2006.881948
Monga V, Banerjee A, Evans BL: A clustering based approach to perceptual image hashing. IEEE Transactions on Information Forensics and Security 2006, 1(1):68-79. 10.1109/TIFS.2005.863502
Johnson M, Ramchandran K: Dither-based secure image hashing usng distributed coding. Proceedings of the International Conference on Image Processing (ICIP '03), September 2003, Barcelona, Spain 3: 751-754.
Lefbvre F, Czyz J, Macq B: A robust soft hash algorithm for digital image signature. Proceedings of the IEEE International Conference on Image Processing (ICIP '03), September 2003, Barcelona, Spain 2: 495-498.
Mihcak K, Venkatesan R: New iterative geometric techniques for robust image hashing. Proceedings of the ACM Workshop in Security and Privacy in Digital Rights Management, November 2001, Philadelphia, Pa, USA 13-21.
Kozat SS, Venkatesan R, Mihcak MK: Robust perceptual image hashing via matrix invariants. Proceedings of the IEEE International Conference on Image Processing (ICIP '04), October 2004, Singapore 5: 3443-3446.
Lee D, Seung H: Algorithms for non-negative matrix factorization. Advances in Neural Information Processing Systems 2001, 13: 556-562.
Monga V, Mihcak MK: Robust and secure image hashing via non-negative matrix factorizations. IEEE Transactions on Information Forensics and Security 2007, 2(3):376-390. 10.1109/TIFS.2007.902670
Guillamet D, Schiele B, Vitria J: Analyzing non-negative matrix factorization for image classification. Proceedings of the International Conference on Pattern Recognition, August 2002, Quebec, Canada 16: 116-119.
Ailon N, Chazelle B: Approximate nearest neighbors and the fast johnson-lindenstrauss transform. Proceedings of the 38st Annual Symposium on the Theory of Computing (STOC '06), 2006, Seattle, Wash, USA 557-563.
Lv X, Wang Z: Fast Johnson-Lindenstrauss transform for robust and secure image hashing. Proceedings of the IEEE 10th Workshop on Multimedia Signal Processing, October 2008, Cairns, Australia 725-729.
Lin C, Wu M, Bloom J, et al.: Rotation, scale, and translation resilient watermarking for images. IEEE Transactions on Image Processing 2001, 10(5):767-782. 10.1109/83.918569
Cover T, Thomas J, Wiley J, InterScience W: Elements of Information Theory. Wiley-Interscience, New York, NY, USA; 2006.
International Computer Science Institute,Dasgupta S, Gupta A: An elementary proof of the Johnson-Lindenstrauss lemma. International Computer Science Institute; 1999.
Fawcett T: An introduction to ROC analysis. Pattern Recognition Letters 2006, 27(8):861-874. 10.1016/j.patrec.2005.10.010
Alghoniemy M, Tewfik AH: Geometric invariance in image watermarking. IEEE Transactions on Image Processing 2004, 13(2):145-153. 10.1109/TIP.2004.823831
Bishop C: Pattern Recognition and Machine Learning. Springer, New York, NY, USA; 2006.
Jain A, Nandakumar K, Ross A: Score normalization in multimodal biometric systems. Pattern Recognition 2005, 38(12):2270-2285. 10.1016/j.patcog.2005.01.012
Mao Y, Wu M: Unicity distance of robust image hashing. IEEE Transactions on Information Forensics and Security 2007, 2(3, part 1):462-467. 10.1109/TIFS.2007.902260
Shih FY, Wu Y: Enhancement of image watermark retrieval based on genetic algorithms. Journal of Visual Communication and Image Representation 2005, 16(2):115-133. 10.1016/j.jvcir.2004.05.002
Shieh CS, Huang HC, Wang FH, Pan JS: Genetic watermarking based on transform-domain techniques. Pattern Recognition 2004, 37(3):555-565. 10.1016/j.patcog.2003.07.003
Chu S, Huang H, Shi Y, Wu S, Shieh C: Genetic watermarking for zerotree-based applications. Circuits, Systems, and Signal Processing 2008, 27(2):171-182. 10.1007/s00034-008-9025-z
Fatourechi M, Lv X, Wang ZJ: Towards fast automated image hashing based on fast johnson-lindenstrauss transform (fjlt). Proceedings of the IEEE International Workshop on Information Forensics and Security, December 2009, London, UK
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lv, X., Wang, Z. An Extended Image Hashing Concept: Content-Based Fingerprinting Using FJLT. EURASIP J. on Info. Security 2009, 859859 (2009). https://doi.org/10.1155/2009/859859
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/859859

 .
.
 ) when employing ordered random weighting and unordered random weighting. OrderedUnordered
) when employing ordered random weighting and unordered random weighting. OrderedUnordered

 . (c) Original Goldhill in Log-Polar coordinates. (d) Rotated Goldhill in Log-Polar coordinates.
. (c) Original Goldhill in Log-Polar coordinates. (d) Rotated Goldhill in Log-Polar coordinates.



 NMF on
NMF on 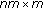 matrices and then a rank
matrices and then a rank 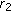 approximation from the resulting
approximation from the resulting  matrix in [
matrix in [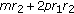 , and the total computation cost is
, and the total computation cost is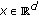 , the computation cost of FJLT on
, the computation cost of FJLT on  is calculated as follows. Computing
is calculated as follows. Computing  requires
requires  time and
time and  requires
requires 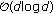 . For computing
. For computing 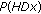 , it takes
, it takes 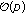 , where the
, where the  is the number of nonzeros in
is the number of nonzeros in  , we know that the
, we know that the 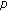 satisfies the Binomial distribution
satisfies the Binomial distribution  , therefore we take the mean value of
, therefore we take the mean value of 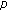 as
as 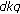 that equals
that equals 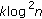 , where
, where 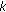 is
is 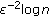 . Then, take the random weight incorporation into account, we have the total computation cost of the FJLT hashing as (
. Then, take the random weight incorporation into account, we have the total computation cost of the FJLT hashing as (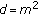 in our case)
in our case) and Fourier transform that takes
and Fourier transform that takes  by FFT into account. Consequently, the cost of RI-FJLT is
by FFT into account. Consequently, the cost of RI-FJLT is